[Python][Physics]#10 복소수 표현을 사용한 삼각함수의 곱셈 공식(시각화)

수식: 

 

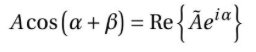
이 수식은 복소수 표현을 사용하여 삼각함수의 곱셈 공식을 나타내고 있습니다. 이 수식을 자세히 살펴보겠습니다.

1. 이식이 나타내는 것: 수식은 cos(α+β)를 A와 관련된 복소수 표현식으로 나타낸 것입니다. 여기서 A는 cos(α+β)의 계수이며, α와 β는 각각의 각도입니다. 이 수식은 cos(α+β)와 A * e^(iα)의 실수부 Re{A * e^(iα)} 사이의 관계를 보여줍니다.
2. 이식의 목적과 의미: 이 수식의 목적은 삼각함수의 곱셈 공식을 복소수 형태로 나타내어 복소수 표현을 이용한 삼각함수의 성질과 관계를 보다 쉽게 이해하고 분석할 수 있도록 하는 것입니다. 이를 통해 삼각함수와 복소수 사이의 연결고리를 확인할 수 있으며, 복소수를 이용한 수학적 문제를 다루는 데 도움이 됩니다.
3. 활용 방안: 이 공식은 다양한 분야에서 삼각함수와 복소수를 함께 다루는 문제를 해결하는 데 사용됩니다. 예를 들어, 전자공학, 통신, 신호 처리 등의 분야에서 주기적인 신호를 분석하거나 변환하는 데 이 공식이 사용될 수 있습니다. 또한 이 공식은 복소수를 이용한 적분, 미분, 해석학 등의 수학적 연구에서 삼각함수의 성질과 관계를 파악하는 데 도움이 됩니다.
4. Code:

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# Parameters
A = 1
alpha_range = np.linspace(0, 2 * np.pi, 100)
beta_range = np.linspace(0, 2 * np.pi, 100)

# Function for Acos(α+β) = Re{A*e^(i*α)}
def rotated_vector(A, alpha, beta):
    z = A * np.cos(alpha + beta)
    x = z * np.cos(alpha)
    y = z * np.sin(alpha)
    return x, y, z

# Prepare 3D grid
alpha_grid, beta_grid = np.meshgrid(alpha_range, beta_range)
x_grid, y_grid, z_grid = rotated_vector(A, alpha_grid, beta_grid)

# Plot the surface
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
surface = ax.plot_surface(x_grid, y_grid, z_grid, cmap='viridis', alpha=0.8)

# Add labels and legend
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
fig.colorbar(surface, ax=ax, label='Acos(α+β) = Re{A*e^(i*α)}')

plt.show()

 

 

5. Code 설명 및 결과: 이 코드는 주어진 수식 Acos(α+β) = Re{A*e^(i*α)}를 사용하여 3D 벡터를 시각화합니다. 여기서는 α와 β 값이 0에서 2π 사이로 변하는 것을 가정하고 있습니다.

A: 벡터의 크기를 나타내는 상수입니다.

alpha_range, beta_range: α와 β 값의 범위를 설정합니다. 여기서는 0에서 2π 사이의 값을 가지도록 설정

rotated_vector: 주어진 식에 따라 벡터를 회전시키는 함수입니다. 입력으로 A, α, β를 받고, 출력으로 회전된 벡터의 x, y, z 좌표를 반환합니다.

 

주어진 식에 따라 α와 β 값을 변화시키면서 3D 공간에서 벡터를 회전시키는 과정을 시각화합니다. 이를 통해 복소 평면에서의 벡터 회전을 더 쉽게 이해할 수 있습니다.