[Python][Physics]#06 가우스 발산 정리(Gauss's Divergence Theorem)(시각화)

수식: 

 

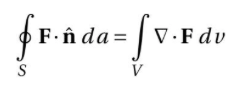
이 식은 벡터장의 플럭스를 계산하는 방법을 나타내며, 가우스 발산 정리(Gauss's Divergence Theorem)라고도 불립니다.

1. 이 식이 나타내는 것:
가우스 발산 정리는 공간적 영역 내에서 벡터장의 발산과 그 영역의 경계면을 따른 벡터장의 플럭스 간의 관계를 나타냅니다. 즉, 공간 영역 V의 경계면 S를 따라 벡터장 F의 플럭스를 적분한 값은, 영역 V 내에서 벡터장 F의 발산을 적분한 값과 같습니다.

2. 이 식의 목적:
가우스 발산 정리의 목적은 다양한 물리적 문제를 해결하는데 도움을 주는 것입니다. 이 정리를 사용하면 복잡한 형상의 영역에 대한 적분을 더 간단한 형태로 변환할 수 있어 계산이 수월해집니다.

3. 이 식의 의미:
이 정리는 벡터장의 발산이 영역 내부에서 발생하는 변화를 측정하는 반면, 플럭스는 영역의 경계를 통해 벡터장이 나가는 양을 측정한다는 것을 보여줍니다. 가우스 발산 정리는 이 두 가지 측정이 균형을 이루어야 함을 나타냅니다. 즉, 영역 내부에서 발생하는 변화의 총량은 영역 경계를 통해 나가는 변화의 총량과 일치해야 합니다.

4. 활용 방안:
가우스 발산 정리는 물리학, 공학, 전산학 등 다양한 분야에서 활용됩니다. 전기장, 자기장, 유체역학, 열전달 등 여러 물리적 문제를 해결하는 데 사용되며, 복잡한 형태의 경계를 가진 영역에 대한 적분 문제를 간단한 형태로 변환하여 계산이 수월해지게 합니다.

 

5. Code:

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 벡터 필드 F 정의
def vector_field(x, y, z):
    Fx = x * y - z
    Fy = y * z + x
    Fz = z * x - y
    return Fx, Fy, Fz

# 발산 계산
def divergence(x, y, z, Fx, Fy, Fz):
    dFx_dx = np.gradient(Fx, axis=0)
    dFy_dy = np.gradient(Fy, axis=1)
    dFz_dz = np.gradient(Fz, axis=2)
    div = dFx_dx + dFy_dy + dFz_dz
    return div

# 3D 그리드 생성
x, y, z = np.meshgrid(np.linspace(-5, 5, 10),
                      np.linspace(-5, 5, 10),
                      np.linspace(-5, 5, 10))

# 벡터 필드와 발산 계산
Fx, Fy, Fz = vector_field(x, y, z)
divergence_field = divergence(x, y, z, Fx, Fy, Fz)

# 시각화
fig = plt.figure(figsize=(12, 6))

# 벡터 필드 시각화
ax1 = fig.add_subplot(121, projection='3d')
ax1.quiver(x, y, z, Fx, Fy, Fz, length=1, color='b', normalize=True)
ax1.set_title("Vector field F")
ax1.set_xlabel("X-axis")
ax1.set_ylabel("Y-axis")
ax1.set_zlabel("Z-axis")

# 발산 시각화
ax2 = fig.add_subplot(122, projection='3d')
ax2.scatter(x, y, z, c=divergence_field.flatten(), cmap='coolwarm', s=20)
ax2.set_title("Divergence of F")
ax2.set_xlabel("X-axis")
ax2.set_ylabel("Y-axis")
ax2.set_zlabel("Z-axis")

plt.show()

 

 

 

6. Code 설명 및 결과:

주어진 벡터 필드 F에 대해 3D 그리드를 만들고, 벡터 필드와 발산을 계산한 후 이를 시각화합니다. 발산은 색상으로 표시되어 있습니다. 이 코드를 사용하여 다양한 벡터 필드를 시각화하고 가우스 발산 정리를 탐색할 수 있습니다. 벡터 필드 함수를 변경하여 다른 벡터 필드를 시각화 할 수 있습니다.