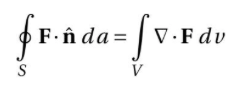수식: 이 식은 벡터장의 플럭스를 계산하는 방법을 나타내며, 가우스 발산 정리(Gauss's Divergence Theorem)라고도 불립니다. 1. 이 식이 나타내는 것: 가우스 발산 정리는 공간적 영역 내에서 벡터장의 발산과 그 영역의 경계면을 따른 벡터장의 플럭스 간의 관계를 나타냅니다. 즉, 공간 영역 V의 경계면 S를 따라 벡터장 F의 플럭스를 적분한 값은, 영역 V 내에서 벡터장 F의 발산을 적분한 값과 같습니다. 2. 이 식의 목적: 가우스 발산 정리의 목적은 다양한 물리적 문제를 해결하는데 도움을 주는 것입니다. 이 정리를 사용하면 복잡한 형상의 영역에 대한 적분을 더 간단한 형태로 변환할 수 있어 계산이 수월해집니다. 3. 이 식의 의미: 이 정리는 벡터장의 발산이 영역 내부에서 발생하는..