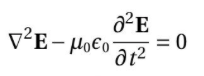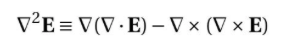Luke's Study Space

수식: 1. 이 식의 의미와 목적: ∇²𝐸 - μ₀ϵ₀(∂²𝐸/∂t²) = 0은 맥스웰의 방정식 중 하나로, 전자기학의 중요한 개념을 나타냅니다. 이 식은 전자기장의 공간적인 변화와 시간적인 변화 간의 관계를 설명하고, 전자기장의 동적인 특성을 나타내는 방정식입니다. 우선, 식 ∇²𝐸 - μ₀ϵ₀(∂²𝐸/∂t²) = 0에서 ∇²𝐸는 전자기장의 공간적인 변화를 측정하는 라플라시안(Laplacian) 연산자입니다. 이 연산자를 이용하여 전자기장의 공간적인 변화에 대한 미분을 계산합니다. 그리고 ∂²𝐸/∂t²는 시간에 대한 전자기장의 두 번째 도함수로, 전자기장의 시간적인 변화율을 측정합니다. 이 식을 통해 전자기장이 시간에 따라 어떻게 변화하는지를 나타낼 수 있습니다. 따라서 식 ∇²𝐸 - μ₀ϵ₀(∂²𝐸/..

수식: 이 식은 벡터 필드인 전기장(Electric Field, E)에 대한 라플라시안(Laplacian) 연산자를 나타냅니다. 라플라시안 연산자는 스칼라와 벡터 필드에 적용할 수 있는 두 번째 차 도함수를 표현하는데 사용되며, 일반적으로 공간적인 변화에 따른 중요한 물리량의 변화를 나타냅니다. 이 식은 다음과 같은 구성 요소로 이루어져 있습니다. 1. 이식이 나타내는 것: 전기장(E)에 대한 라플라시안 연산자(Δ²E)를 계산합니다. 이 연산자는 전기장의 공간적인 변화를 설명하는 데 도움이 됩니다. 2. 목적: 라플라시안 연산자는 여러 분야에서 물리량의 변화를 분석하는 데 사용됩니다. 전기장의 경우, 라플라시안 연산자를 사용하여 전기장의 국지적인 변화를 분석하거나 전기장의 안정성, 불균일성 등을 평가할 ..

해당 파이썬 코드는 전하 크기와 위치에 따라 발생하는 전기장 벡터를 3차원으로 시각화하는 것입니다. 예시 코드에서는 주어진 전기장 벡터 함수를 이용하여 그리드를 생성하고, 그리드 상의 각 점에서의 전기장 벡터를 계산하여 3D 그래프로 표현합니다. 따라서 코드 실행 결과로는 전기장 벡터의 방향과 크기를 보여주는 3D 그래프가 생성됩니다. 수식: code: import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D # 전하 크기와 거리 설정 q = 1 A = 1 # 전기장 함수 def E(x, y, z): r = np.sqrt(x**2 + y**2 + z**2) Ex = q*(1/r**2)*(x/r) Ey..