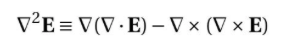Luke's Study Space

수식: 이 식은 벡터 필드인 전기장(Electric Field, E)에 대한 라플라시안(Laplacian) 연산자를 나타냅니다. 라플라시안 연산자는 스칼라와 벡터 필드에 적용할 수 있는 두 번째 차 도함수를 표현하는데 사용되며, 일반적으로 공간적인 변화에 따른 중요한 물리량의 변화를 나타냅니다. 이 식은 다음과 같은 구성 요소로 이루어져 있습니다. 1. 이식이 나타내는 것: 전기장(E)에 대한 라플라시안 연산자(Δ²E)를 계산합니다. 이 연산자는 전기장의 공간적인 변화를 설명하는 데 도움이 됩니다. 2. 목적: 라플라시안 연산자는 여러 분야에서 물리량의 변화를 분석하는 데 사용됩니다. 전기장의 경우, 라플라시안 연산자를 사용하여 전기장의 국지적인 변화를 분석하거나 전기장의 안정성, 불균일성 등을 평가할 ..

수식: 이 수식은 스칼라 함수 f(x, y, z)에 대한 라플라시안(Laplacian) 연산자를 정의한 것입니다. 이 식에서 ∇²f(x, y, z)는 라플라시안 값이며, ∇f(x, y, z)는 함수 f의 그래디언트(gradient) 벡터입니다. 이 식은 다음과 같이 해석할 수 있습니다. 1. 이 식이 나타내는 것: 이 식은 스칼라 함수 f(x, y, z)에 대한 라플라시안 연산자를 나타냅니다. 라플라시안 연산자는 그래디언트 벡터의 발산(divergence)을 계산하여, 스칼라 함수의 두 번째 도함수의 합을 구합니다. 2. 목적: 라플라시안 연산자는 스칼라 함수의 국지적인 특성을 분석하는 데 사용됩니다. 함수의 최대점, 최소점 및 안정점을 찾는데 도움이 됩니다. 3. 의미: 라플라시안 값이 양수인 경우, ..