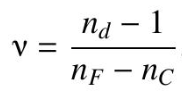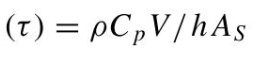Luke's Study Space

수식: 1. 이 식의 의미와 목적: 이 방정식은 Sellmeier 방정식이라고 알려져 있습니다. 이는 유리나 다른 투명한 물질의 굴절률을 묘사하기 위해 사용되는 특별한 형태의 디스퍼젼 방정식입니다. 광학에서, 디스퍼젼은 빛의 속도가 그 파장에 따라 다르게 변하는 현상을 설명하는데 사용됩니다. 특정 물질에서 빛의 속도는 그 물질의 굴절률에 의해 결정됩니다. 따라서 굴절률은 빛의 파장에 따라 변하며, 이 변화는 디스퍼젼을 초래합니다. Sellmeier 방정식의 목적은 굴절률을 파장의 함수로 정확하게 예측하기 위한 것입니다. Sellmeier 계수 B1, B2, B3, lambda1, lambda2, lambda3는 특정 물질의 광학적 특성을 결정하는 실험적으로 얻어진 값입니다. 이 계수들은 물질의 구조와 상..

수식: 1. 이식이 나타내는 의미와 목적: v=(n_d-1)/(n_F-n_C) 식은 Abbe 수(또는 v-수)를 계산하는 식으로, 광학 소재의 분산을 표현하고자 합니다. 이 식을 통해 파장에 따른 굴절률의 변화를 평가할 수 있습니다. 주요 용어 설명: n_d: 특정 파장 (예: 587.3 nm)에서 측정된 광학 소재의 굴절률 n_C: 특정 파장 (예: 656.3 nm)에서 측정된 광학 소재의 굴절률 n_F: 특정 파장 (예: 486.1 nm)에서 측정된 광학 소재의 굴절률 v=(n_d-1)/(n_F-n_C)의 분자는 특정 파장에서의 굴절률과 공기의 굴절률(1)의 차이를 나타냅니다. 분모는 특정 파장에서의 굴절률 변화의 범위를 나타냅니다. 따라서, Abbe 수는 광학 소재가 파장에 따라 굴절률이 얼마나 변..

수식: 1. 이식의 의미와 목적: 여기서 I(λ)는 스펙트럼 또는 파장에 대한 강도를 나타내는 함수이고, x̄, ȳ, z̄는 해당 파장에서의 특정 물리량의 평균값입니다. 또한, ∫는 적분 기호를 나타냅니다. 이러한 식의 의미는 각각의 적분 결과인 X, Y, Z가 파장 범위(λ)에 대해 I(λ) 함수로 가중 평균된 값을 나타낸다는 것입니다. 이러한 식들은 스펙트럼 분석이나 광학 연구에서 자주 사용됩니다. 이러한 적분은 주어진 파장 범위에서의 물리량의 평균을 계산하기 위해 사용됩니다. 일반적으로, 광학 연구에서는 빛의 파장에 따른 특정 물리량의 변화를 이해하고자 합니다. 이를 위해 스펙트럼 분석이 사용되며, 주어진 파장 범위에서의 강도를 나타내는 I(λ) 함수를 사용합니다. 예를 들어, X는 파장 범위 내에..

수식: 1. 이 식의 의미와 목적: U(x, t) = T(t)X(x): 이 식은 분리 변수법을 사용하여 1차원 열 전달 문제의 해를 표현합니다. 분리 변수법은 다변수 함수를 각 변수에 대한 단일 변수 함수의 곱으로 분리하는 수학적인 기법입니다. 이 식에서 U(x, t)는 위치 x와 시간 t에 따른 온도 분포를 나타내는 함수입니다. 분리 변수법을 사용하여 T(t)와 X(x)를 분리하고 각각 시간과 위치에 대한 함수로 표현함으로써 원래의 편미분 방정식을 간단한 형태의 방정식으로 분리합니다. 이를 통해 초기 조건과 경계 조건에 맞는 1차원 열 전달 문제의 해를 구할 수 있습니다. U(x, t) = Ae^(-κt/λ^2) [Bcos(x/λ) + Csin(x/λ) U(x, t) = e^(-κt/λ^2) [Dcos..

수식: 1. 목적과 의미: (τ)=ρC_p V/hA_(S) 식의 목적은 렌즈 주조 공정에서 열 시간 상수(thermal time constant)를 계산하여 열 전달 특성을 평가하는 것입니다. 이 식은 밀도(ρ), 열용량(C_p), 렌즈의 부피(V), 열전달 계수(h), 그리고 표면적(A_S)과 같은 렌즈의 특성에 의존하여 열 시간 상수(τ)를 결정합니다. 이를 통해 렌즈 주조 공정에서 발생하는 열 전달 특성을 종합적으로 평가할 수 있습니다. 2. 수식 기호별 의미: ρ (밀도): 밀도는 렌즈의 단위 체적당 질량을 나타냅니다. 즉, 단위 부피 내에 포함된 렌즈의 질량입니다. 단위는 그램 단위의 질량에 대한 미터 제곱 단위의 부피로 표시됩니다 (g/m^3). C_p (열용량): 열용량은 단위 질량당 열에 ..

수식: lens 주조 공정에서 초기 온도 차이와 열 전달 특성을 이해하고 제어하는 데 도움을 주는 중요한 식입니다. 이를 통해 렌즈의 열 관리와 주조 공정의 최적화를 수행할 수 있습니다 1. 이 식의 목적과 의미 주조 과정에서 발생하는 열 관리와 관련된 문제를 이해하고 해결하는 데 목적이 있습니다. 초기 온도 차이(ΔT₀)와 열 시간 상수(τ)를 고려하여 렌즈 주조 과정의 열 전달과 열 변화를 모델링하고 예측하는 데 활용됩니다. 목표는 원하는 렌즈 속성을 얻기 위해 적절한 열 관리 방법을 설계하고 주조 공정을 최적화하는 것입니다 ΔT(t) = ΔT₀e^(-t/τ) 식은 주조 시간(t)에 따른 온도 변화(ΔT)를 나타내며, 주조 과정에서 열 전달과 관련된 초기 조건과 열 전달 특성을 고려합니다. 초기 온도..

수식: 이 식은 빛의 파동수와 관련된 파동수 벡터인 k와 광학 매체의 성질을 나타내는 ϵ₀, μ₀, χ(ω) 간의 관계를 설명합니다. 이를 통해 주어진 주파수(ω)에서의 굴절률을 계산할 수 있습니다. 1. 이식의 의미와 목적: 이 식은 전자기학에서의 굴절률(refractive index)을 이론적으로 설명하는 식입니다. 굴절률은 빛이 한 매질에서 다른 매질로 전파될 때 경로를 변경하는 현상을 나타냅니다. 식을 살펴보면, 우선 좌변의 k²는 빛의 파동수에 대한 파동수 벡터의 제곱을 의미합니다. 이는 빛의 파동이 얼마나 "길게" 전파되는지를 나타내는 값입니다. 우변의 ϵ₀는 진공의 유전율을 나타내며, μ₀는 진공의 자기율을 나타냅니다. 이는 진공 상태에서의 빛의 전파 특성을 기술하는 상수입니다. 식의 나머지..

수식: 이 식은 전자기파의 공간적인 변화와 시간적인 진동을 나타내며, 전자기파의 전기장 벡터 크기와 방향은 위치 r과 시간 t에 따라 변화한다는 것입니다.. 1. 의미와 목적: 이 식은 전자기파의 전기장 벡터를 나타내는 식으로, 전자기파의 공간적인 변화와 시간적인 진동을 표현합니다. 전자기파는 전자기력이나 광학 등 다양한 분야에서 중요한 역할을 합니다. 이 식은 전자기파의 특성을 수학적으로 설명하고 예측하는 데 사용됩니다. 복소 지수 형태인 e^(i(kr - wt))를 가지고 있습니다. 복소 지수 형태는 삼각함수와 지수함수의 관계를 나타내는 오일러 공식에 기반합니다. 전자기파의 전기장 벡터는 시간적인 진동과 공간적인 변화를 동시에 나타내기 위해 복소 지수 형태로 표현됩니다. kr은 위치 벡터 r과 파동수..

수식: 평면파 식은 위치 r에서 시간 t일 때의 전기장의 크기와 방향을 나타내는 벡터를 나타내는 수식입니다. 1. 식의 의미: E(r,t) = E₀cos(k⋅r - ωt + ϕ)은 전자기학에서 사용되는 전자기장의 시간과 위치에 대한 함수입니다. 이 식에서 E₀는 전자기장의 최대 크기를 나타내며, k는 전파의 파동수를 결정하는 파동수 벡터, r은 위치 벡터, ω는 각주파수를 나타내는 각속도, t는 시간, 그리고 ϕ는 초기 위상입니다. 이 식은 일반적으로 평면파를 나타내는데 사용됩니다. 즉, 전자기파가 일정한 파동수와 진폭으로 퍼져나가는 경우에 이 식을 사용할 수 있습니다. 이러한 전자기파는 빛, 라디오, TV 등의 통신에서 사용됩니다. 이 식의 목적은 전자기장의 크기와 방향을 설명하는 것입니다. E₀는 전..

수식: 주어진 식 ∇×(∇×E) + ∂/∂t(∇×B) = 0 은 맥스웰의 파동방정식 중 하나로, 전자기장의 시간 변화와 전류 밀도의 변화를 설명하는데 사용됩니다. 이 방정식은 전자기장이 어떻게 변화하는지를 나타내며, 전자기파의 전달과 같은 많은 물리적 현상을 설명하는 데 사용됩니다. 1. 이식의 의미: 맥스웰의 파동방정식 중 하나인 ∇×(∇×E) + ∂/∂t(∇×B) = 0 이식은, 전자기장의 시간적 변화와 전류 밀도의 변화가 서로 연관되어 있다는 것을 나타내며, 전자기파의 전달과 같은 많은 물리적 현상을 설명하는 데 사용됩니다. 이를 이해하기 위해서는 전자기장이 무엇인지를 먼저 이해해야 합니다. 전자기장은 전기와 자기의 상호작용으로 발생하는 벡터장으로, 전자의 운동, 전기장과 자기장에 의한 힘, 전류 ..