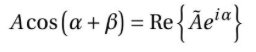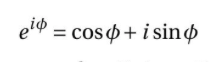Luke's Study Space

수식: 이 수식은 복소수 표현을 사용하여 삼각함수의 곱셈 공식을 나타내고 있습니다. 이 수식을 자세히 살펴보겠습니다. 이식이 나타내는 것: 수식은 cos(α+β)를 A와 관련된 복소수 표현식으로 나타낸 것입니다. 여기서 A는 cos(α+β)의 계수이며, α와 β는 각각의 각도입니다. 이 수식은 cos(α+β)와 A * e^(iα)의 실수부 Re{A * e^(iα)} 사이의 관계를 보여줍니다. 이식의 목적과 의미: 이 수식의 목적은 삼각함수의 곱셈 공식을 복소수 형태로 나타내어 복소수 표현을 이용한 삼각함수의 성질과 관계를 보다 쉽게 이해하고 분석할 수 있도록 하는 것입니다. 이를 통해 삼각함수와 복소수 사이의 연결고리를 확인할 수 있으며, 복소수를 이용한 수학적 문제를 다루는 데 도움이 됩니다. 활용 방..

수식: 이 수식은 복소수에서 쌍곡선 사인(hyperbolic sine, sinh)과 쌍곡선 코사인(hyperbolic cosine, cosh) 함수를 유도하는 공식을 나타냅니다. 이 수식을 자세히 살펴보겠습니다. 이식이 나타내는 것: 이 수식은 복소수 공간에서 쌍곡선 사인 함수와 쌍곡선 코사인 함수를 유도하는 공식입니다. 이 공식에 따르면, 쌍곡선 사인 함수 sinh(γ)는 복소수 i와 각 γ의 곱의 사인 함수 sin(iγ)와 관련되어 있습니다. 마찬가지로, 쌍곡선 코사인 함수 cosh(γ)는 복소수 i와 각 γ의 곱의 코사인 함수 cos(iγ)와 관련되어 있습니다. 이식의 목적과 의미: 이 공식의 목적은 복소수에서의 삼각함수와 쌍곡선 함수 사이의 관계를 설명하는 것입니다. 이 관계를 통해 복소수 영역에..

수식: 이 식은 오일러 공식(Euler's formula)이라고도 불리며, e, i, pi, cos, sin 등 다양한 수학적 개념이 하나로 합쳐진 식입니다. 1. 이식이 나타내는 것: 이 식은 e, i, pi, cos, sin 등의 수학적 개념을 하나의 식으로 표현하여 수학적인 계산을 단순하게 만들어 주는 역할을 합니다. 또한 이 식은 삼각함수와 지수함수를 연결시켜주는 중요한 역할을 하며, 물리학, 공학, 수학 등 다양한 분야에서 활용되고 있습니다. 2. 목적: e^iϕ=cos⁡ϕ+isin⁡ϕ 이식은 삼각함수와 지수함수를 연결시켜주는 역할을 하므로, 다음과 같은 의미와 활용 방안을 갖습니다. 3. 의미: - 복소수의 지수 표현: e^(ix)는 복소평면 상에서 각도 x에 해당하는 위치의 복소수를 의미합니..