[Python][Physics]#04 스칼라 함수 f(x, y, z)에 대한 라플라시안(Laplacian) 연산자 정의(시각화)

수식:

 

이 수식은 스칼라 함수 f(x, y, z)에 대한 라플라시안(Laplacian) 연산자를 정의한 것입니다. 이 식에서 ∇²f(x, y, z)는 라플라시안 값이며, ∇f(x, y, z)는 함수 f의 그래디언트(gradient) 벡터입니다. 이 식은 다음과 같이 해석할 수 있습니다.

1. 이 식이 나타내는 것: 이 식은 스칼라 함수 f(x, y, z)에 대한 라플라시안 연산자를 나타냅니다. 라플라시안 연산자는 그래디언트 벡터의 발산(divergence)을 계산하여, 스칼라 함수의 두 번째 도함수의 합을 구합니다.

2. 목적: 라플라시안 연산자는 스칼라 함수의 국지적인 특성을 분석하는 데 사용됩니다. 함수의 최대점, 최소점 및 안정점을 찾는데 도움이 됩니다.

3. 의미: 라플라시안 값이 양수인 경우, 함수의 국지적인 최소점을 나타낼 수 있습니다. 이 경우 함수는 국지적으로 볼록한(convex) 영역에 있을 가능성이 높습니다. 라플라시안 값이 음수인 경우, 함수의 국지적인 최대점을 나타낼 수 있습니다. 이 경우 함수는 국지적으로 오목한(concave) 영역에 있을 가능성이 높습니다. 라플라시안 값이 0인 경우, 함수는 안정점(정류점)이거나 안정점 근처에 있을 가능성이 있습니다.

4. 활용방안: 라플라시안 연산자를 사용하여 스칼라 함수의 국지적인 특성을 분석하면, 함수의 극값을 찾거나 함수의 변화를 이해하는 데 도움이 됩니다. 이를 통해 온도, 압력, 밀도 등 물리량의 분포와 변화를 연구할 수 있습니다. 또한 라플라시안 연산자는 고유값 문제와 편미분 방정식에서 주요 역할을 하여, 수학적 모델링과 엔지니어링 문제 해결에 활용됩니다.

 

5. Code:

 

import numpy as np

import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d import Axes3D

def f(x, y, z):

return x**2 + y**2 + z**2

x = np.linspace(-10, 10, 50)

y = np.linspace(-10, 10, 50)

z = np.linspace(-10, 10, 50)

x, y, z = np.meshgrid(x, y, z)

scalar_field = f(x, y, z)

# Flatten the arrays for scatter plot

x = x.flatten()

y = y.flatten()

z = z.flatten()

scalar_field = scalar_field.flatten()

fig = plt.figure()

ax = fig.add_subplot(111, projection='3d')

cmap = plt.get_cmap('viridis')

norm = plt.Normalize(scalar_field.min(), scalar_field.max())

colors = cmap(norm(scalar_field))

ax.scatter(x, y, z, c=colors, s=2) # s is the marker size, you can adjust it as needed

m = plt.cm.ScalarMappable(cmap=cmap, norm=norm)

m.set_array([])

cbar = plt.colorbar(m)

cbar.set_label('f(x, y, z)')

ax.set_xlabel('X')

ax.set_ylabel('Y')

ax.set_zlabel('Z')

plt.show()

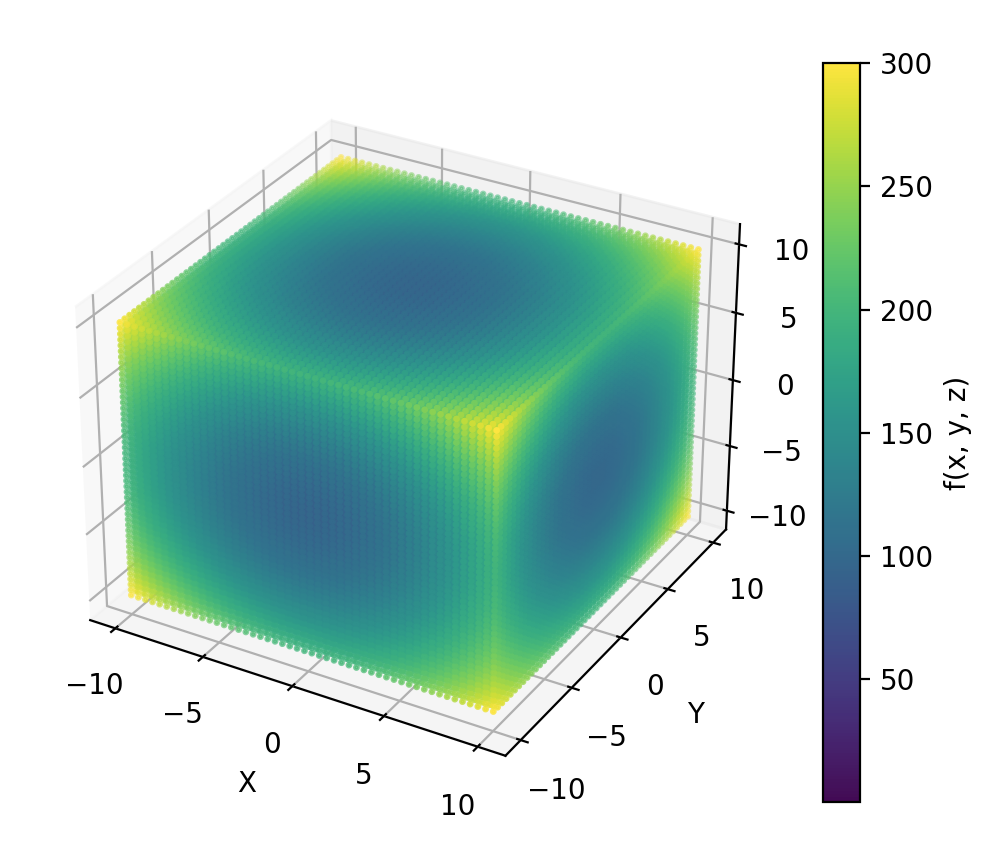
6. code 설명 및 결과: 3D 스칼라 함수 f(x, y, z)를 시각화하는 예제입니다. 여기서는 f(x, y, z) = x^2 + y^2 + z^2 라는 간단한 함수를 사용하였습니다. 이 예제에서는 Matplotlib와 NumPy 라이브러리를 사용하여 그래프를 생성합니다. f(x, y, z) = x^2 + y^2 + z^2 의 값을 3D 공간에 색상으로 표시한 그래프를 생성합니다. 범례(컬러바)는 f(x, y, z) 값을 나타내며, X, Y, Z 레이블이 각 축에 표시됩니다