수식:
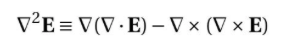
이 식은 벡터 필드인 전기장(Electric Field, E)에 대한 라플라시안(Laplacian) 연산자를 나타냅니다. 라플라시안 연산자는 스칼라와 벡터 필드에 적용할 수 있는 두 번째 차 도함수를 표현하는데 사용되며, 일반적으로 공간적인 변화에 따른 중요한 물리량의 변화를 나타냅니다. 이 식은 다음과 같은 구성 요소로 이루어져 있습니다.
1. 이식이 나타내는 것: 전기장(E)에 대한 라플라시안 연산자(Δ²E)를 계산합니다. 이 연산자는 전기장의 공간적인 변화를 설명하는 데 도움이 됩니다.
2. 목적: 라플라시안 연산자는 여러 분야에서 물리량의 변화를 분석하는 데 사용됩니다. 전기장의 경우, 라플라시안 연산자를 사용하여 전기장의 국지적인 변화를 분석하거나 전기장의 안정성, 불균일성 등을 평가할 수 있습니다.
3. 의미: 라플라시안 연산자는 전기장의 공간적 변화를 측정하는 도구로서, 전기장이 어떻게 분포되어 있는지와 주변 환경에 어떤 영향을 미치는지에 대한 정보를 제공합니다.
4. 활용방안: 라플라시안 연산자는 다양한 물리학과 공학 분야에서 활용됩니다. 전기장의 라플라시안 연산자는 전기장의 분포와 변화를 분석하여, 다양한 전기장 문제를 해결하는 데 도움이 됩니다. 예를 들어, 전기장의 균일성을 확인하거나 전기장 경계 문제를 해결하는 데 사용할 수 있습니다. 또한, 전자기 유도에 의한 전기장의 전달 특성을 연구하는데 사용되기도 합니다.
5. Code:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def electric_field(x, y, z):
E_x = x
E_y = y
E_z = z
return E_x, E_y, E_z
def curl(vx, vy, vz, dx, dy, dz):
curl_x = np.gradient(vz, dy, axis=1) - np.gradient(vy, dz, axis=2)
curl_y = np.gradient(vx, dz, axis=2) - np.gradient(vz, dx, axis=0)
curl_z = np.gradient(vy, dx, axis=0) - np.gradient(vx, dy, axis=1)
return curl_x, curl_y, curl_z
def divergence(vx, vy, vz, dx, dy, dz):
div_x = np.gradient(vx, dx, axis=0)
div_y = np.gradient(vy, dy, axis=1)
div_z = np.gradient(vz, dz, axis=2)
return div_x + div_y + div_z
def laplacian_vector_field(x, y, z, dx, dy, dz):
E_x, E_y, E_z = electric_field(x, y, z)
div_E = divergence(E_x, E_y, E_z, dx, dy, dz)
grad_div_E = np.gradient(div_E, dx, axis=0), np.gradient(div_E, dy, axis=1), np.gradient(div_E, dz, axis=2)
curl_E_x, curl_E_y, curl_E_z = curl(E_x, E_y, E_z, dx, dy, dz)
curl_curl_E = curl(curl_E_x, curl_E_y, curl_E_z, dx, dy, dz)
laplacian_E_x = grad_div_E[0] - curl_curl_E[0]
laplacian_E_y = grad_div_E[1] - curl_curl_E[1]
laplacian_E_z = grad_div_E[2] - curl_curl_E[2]
return laplacian_E_x, laplacian_E_y, laplacian_E_z
x = np.linspace(-5, 5, 10)
y = np.linspace(-5, 5, 10)
z = np.linspace(-5, 5, 10)
dx, dy, dz = x[1] - x[0], y[1] - y[0], z[1] - z[0]
x, y, z = np.meshgrid(x, y, z)
laplacian_E_x, laplacian_E_y, laplacian_E_z = laplacian_vector_field(x, y, z, dx, dy, dz)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.quiver(x, y, z, laplacian_E_x, laplacian_E_y, laplacian_E_z, length=0.5, normalize=True)
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
ax.set_zlabel('Z-axis')
plt.show()
6. Code 설명 및 결과:
1) curl 함수: 입력된 벡터 필드의 컬을 계산합니다.
2) divergence 함수: 입력된 벡터 필드의 발산을 계산합니다.
3) laplacian_vector_field 함수: 이 함수에서는 먼저 전기장의 발산과 컬을 계산한 다음, 주어진 식에 따라 벡터 라플라시안을 계산합니다.
이 코드를 실행하면, 주어진 식에 따른 벡터 라플라시안을 3D로 시각화할 수 있습니다

'[Python][Physics]' 카테고리의 다른 글
| [Python][Physics]#07 스토크스 정리(Stokes' theorem)(시각화) (0) | 2023.05.05 |
|---|---|
| [Python][Physics]#06 가우스 발산 정리(Gauss's Divergence Theorem)(시각화) (0) | 2023.05.04 |
| [Python][Physics]#04 스칼라 함수 f(x, y, z)에 대한 라플라시안(Laplacian) 연산자 정의(시각화) (0) | 2023.05.04 |
| [Python][Physics]#03 전기장 벡터 E의 회전 또는 회전 크기(시각화) (3) | 2023.05.04 |
| [Python][Physics]#02 전기장 벡터의 3차원(시각화) (2) | 2023.05.04 |