수식:
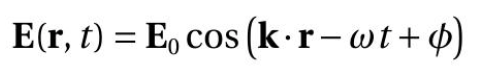
평면파 식은 위치 r에서 시간 t일 때의 전기장의 크기와 방향을 나타내는 벡터를 나타내는 수식입니다.
1. 식의 의미:
E(r,t) = E₀cos(k⋅r - ωt + ϕ)은 전자기학에서 사용되는 전자기장의 시간과 위치에 대한 함수입니다. 이 식에서 E₀는 전자기장의 최대 크기를 나타내며, k는 전파의 파동수를 결정하는 파동수 벡터, r은 위치 벡터, ω는 각주파수를 나타내는 각속도, t는 시간, 그리고 ϕ는 초기 위상입니다.
이 식은 일반적으로 평면파를 나타내는데 사용됩니다. 즉, 전자기파가 일정한 파동수와 진폭으로 퍼져나가는 경우에 이 식을 사용할 수 있습니다. 이러한 전자기파는 빛, 라디오, TV 등의 통신에서 사용됩니다.
이 식의 목적은 전자기장의 크기와 방향을 설명하는 것입니다. E₀는 전자기장의 크기를 결정하고, k는 전파의 파동수와 진폭을 결정합니다. r은 전자기장이 존재하는 위치를 나타내며, t는 시간을 나타내며, ϕ는 초기 위상을 나타냅니다. 이러한 변수들은 전자기장이 어떻게 변하는지 이해하는 데 필요합니다.
따라서, 이 식은 전자기학에서 전자기장의 크기와 방향을 설명하는 데 사용되며, 일정한 파동수와 진폭으로 전자기파가 퍼져나가는 경우에도 유용합니다.
2. 수학기호:
- E(r,t): 위치 r에서 시간 t일 때의 전기장 벡터
- E₀: 최대 전기장 크기, 즉 진폭(amplitude)
- cos(): 코사인 함수
- k: 파수(wavenumber), k = 2π/λ로, 파장 λ의 역수로 공간에서 한 주기당 진동수가 몇 번 반복되는지를 나타냄
- r: 위치 벡터(position vector)
- ω: 각진동수(angular frequency), ω = 2πf로, 일정한 시간 간격으로 진동수가 몇 번 반복되는지를 나타냄
- t: 시간(time)
- ϕ: 위상 상수(phase constant), 각진동수 ω와 시간 t가 0일 때의 위상차(phase difference)를 나타냄
3. 활용 방안:
전자기학에서 많이 사용되며, 전자기장의 성질과 전파의 특성을 이해하는 데 중요한 수식입니다.
전자기장의 진폭, 파수, 각진동수 등을 조절하여 다양한 전자기장의 특성을 모사하고 설계할 수 있습니다.
전파의 특성을 분석하고 예측하는 데 활용됩니다. 예를 들어, 전자기파의 진폭과 주파수를 조절하여 특정 주파수에서 고객의 요구사항에 따라 통신량을 최적화할 수 있습니다.
광학적인 특성을 분석하고 설계하는 데도 활용됩니다. 예를 들어, 레이저의 전기장 분포를 평면파 식을 이용하여 모사하고, 레이저 빔의 강도와 위상을 조절하여 다양한 광학적인 효과를 구현할 수 있습니다.
물리학의 기초적인 이론 중 하나인 맥스웰 방정식(Maxwell's equations)에서 중요한 역할을 합니다. 이 식은 맥스웰 방정식을 통해 파동이 어떻게 전파되는지를 설명하며, 많은 전자기학적인 현상을 설명하는 기초적인 수식 중 하나입니다.
이론적인 분석뿐만 아니라 실험적인 연구에도 활용됩니다. 실험 결과를 분석할 때, 전기장의 크기와 위상을 나타내는 전자기파의 특성을 측정하고 분석할 수 있습니다. 이를 통해 전자기파가 특정한 매질에서 전파되는 방식을 이해하고 실험 결과를 해석할 수 있습니다.
- 통신 분야: 라디오, TV, 휴대전화 등에서 사용되는 전자기파를 설명하는 데 사용됩니다. 이를 통해 통신 기술의 발전과 무선 통신의 구축에 큰 기여를 하고 있습니다.
- 의료 분야: 전자기장이 의료 분야에서도 중요한 역할을 합니다. 자기공명영상(MRI) 기술에서 사용됩니다. MRI는 강한 자기장과 전자기파를 사용하여 인체 내부의 이미지를 생성하는 기술입니다.
- 물리학 분야: 물리학 분야에서도 사용됩니다. 예를 들어, 이 식은 광학적인 상호작용, 레이저와 같은 광원, 광섬유 통신 등에서 사용됩니다.
- 공학 분야: 전기공학, 전자공학, 기계공학 등의 공학 분야에서도 사용됩니다. 이 식은 전자기장의 크기와 방향을 결정하는 데 사용되며, 전자기장이 있는 장소에서 전자를 이동시키는 등 다양한 기술적인 문제를 해결하는 데 사용됩니다.
- 환경 분야: 전자기장은 환경 문제와 관련이 있습니다. 전자기장이 인간 건강에 미치는 영향 등 환경 문제와 관련된 문제를 해결하는 데 사용됩니다. 예를 들어, 전기력선을 설치할 때, 인간 건강에 미치는 영향을 고려하기 위해 전자기장을 측정하는 데 이 식이 사용됩니다.
이처럼, E(r,t) = E₀cos(k⋅r - ωt + ϕ) 식은 다양한 분야에서 다양한 활용 방안이 있습니다. 이를 적극적으로 활용함으로써 새로운 기술 및 제품 개발, 새로운 연구 분야 개척 등에 큰 기여를 할 수 있습니다. 예를 들어, 전자기장이 인체에 미치는 영향을 연구하는 분야에서 이 식을 사용하여 전자기장이 인체에 미치는 영향을 조절하는 기술을 개발할 수 있습니다. 또한, 이 식을 사용하여 더 나은 통신 기술을 개발하거나, 전자기장이 물질에 미치는 영향을 연구하여 새로운 물리 현상을 발견하는 등 다양한 연구 분야에서 적극적으로 활용할 수 있습니다.
또한, 전자기장이 시간과 위치에 따라 어떻게 변하는지를 설명하는데 사용됩니다. 이를 바탕으로 전자기장이 변화하는 과정을 모델링하고 시뮬레이션하는데 사용할 수 있습니다. 이를 통해 다양한 시나리오에서 전자기장이 어떻게 동작하는지 이해하고, 새로운 기술 및 제품 개발에 적용할 수 있습니다.
마지막으로, 전자기학에서 가장 기본적인 식 중 하나입니다. 이를 이해하고 활용하는 것은 전자기학을 이해하는 데 매우 중요합니다. 따라서, 전자기학을 전공하는 학생들은 이 식을 꼭 숙지하고, 다양한 분야에서의 활용 방안을 연구하여 자신의 분야에서 적극적으로 활용할 수 있도록 노력해야 합니다.
4. Code:
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 파라미터 설정
E0 = 1.0
k = 2.0 * np.pi
w = 2.0 * np.pi
phi = 0.0
# x, y, t 그리드 생성
x = np.linspace(-1, 1, 100)
y = np.linspace(-1, 1, 100)
t = 0.0 # 시간을 0으로 초기화
x, y = np.meshgrid(x, y)
# r은 공간 벡터입니다. 일차원에서는 x와 같습니다.
r = np.sqrt(x**2 + y**2)
# 평면파 E(r, t)
E = E0 * np.cos(k * r - w * t + phi)
# 그래프 생성
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# 평면파 그래프 그리기
ax.plot_surface(x, y, E, cmap='viridis')
# 축 라벨 설정
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('E(r, t)')
# 그래프 보여주기
plt.show()
5. Code 설명 및 결과:
3차원 공간에서의 평면파의 수식입니다. 이 식은 r, t, 그리고 여러 상수들의 함수입니다. r은 3차원 공간에서의 위치 벡터이고, t는 시간입니다. k는 파동수, 즉 파장 길이의 역수를 나타내며, ω는 각주파수(angular frequency)를 나타냅니다. ϕ는 초기 위상(constant phase offset)입니다. E₀는 전자기파의 진폭(amplitude)입니다.
이 코드에서는 x, y, E 값을 사용하여 3D 그래프를 그립니다. 이 그래프는 x-y 평면에서의 모양을 보여주는데, 이 모양은 cos 함수의 그래프와 유사합니다. 그리고 축 라벨을 설정하여 x, y, E 값이 각각 어떤 것을 나타내는지 알 수 있도록 합니다.

'[Python][Physics]' 카테고리의 다른 글
| [Python][Physics]#22 전자기학식에서의 굴절율과 χ(ω) 관계(시각화) (0) | 2023.05.12 |
|---|---|
| [Python][Physics]#21 복소 지수 형태의 전자기파 파동식 해석(시각화) (0) | 2023.05.11 |
| [Python][Physics]#19 Maxwell 방정식의 파동 방정식(Wave Equation)(시각화) (0) | 2023.05.10 |
| [Python][Physics]#18 입자 분포 밀도와 자유 입자 밀도의 합산으로 나타낸 총 밀도 함수(시각화) (0) | 2023.05.09 |
| [Python][Physics]#17 Ampere's law의 전류 밀도에 따른 자기장 회전(시각화) (0) | 2023.05.08 |