수식:

주어진 식 ∇×(∇×E) + ∂/∂t(∇×B) = 0 은 맥스웰의 파동방정식 중 하나로, 전자기장의 시간 변화와 전류 밀도의 변화를 설명하는데 사용됩니다. 이 방정식은 전자기장이 어떻게 변화하는지를 나타내며, 전자기파의 전달과 같은 많은 물리적 현상을 설명하는 데 사용됩니다.
1. 이식의 의미:
맥스웰의 파동방정식 중 하나인 ∇×(∇×E) + ∂/∂t(∇×B) = 0 이식은, 전자기장의 시간적 변화와 전류 밀도의 변화가 서로 연관되어 있다는 것을 나타내며, 전자기파의 전달과 같은 많은 물리적 현상을 설명하는 데 사용됩니다.
이를 이해하기 위해서는 전자기장이 무엇인지를 먼저 이해해야 합니다. 전자기장은 전기와 자기의 상호작용으로 발생하는 벡터장으로, 전자의 운동, 전기장과 자기장에 의한 힘, 전류 등의 물리적 현상을 설명하는 데 사용됩니다.
∇×(∇×E) + ∂/∂t(∇×B) = 0 이식은 이러한 전자기장이 어떻게 변화하는지를 나타내는데, 이는 전자기장의 시간 변화와 전류 밀도의 변화가 서로 연관되어 있다는 것을 의미합니다.
예를 들어, 전류가 변화하면 자기장도 변화하게 되며, 이 자기장 변화는 다시 전기장의 변화를 일으킵니다. 이러한 변화는 전자기파의 전달과 같은 많은 물리적 현상을 설명하는 데 사용됩니다.
따라서, 맥스웰의 파동방정식 중 이식은 전자기장의 변화와 전류 밀도의 변화가 서로 연관되어 있으며, 이를 통해 전자기파의 전달과 같은 많은 물리적 현상을 설명할 수 있다는 것을 나타냅니다. 이는 전자기장의 특성을 이해하고, 전자기파를 설계하고 제어하는 기술을 개발하는 데 중요한 역할을 합니다.
이러한 방식으로 맥스웰의 파동방정식은 다양한 분야에서 활용됩니다. 이를 통해 전자기장의 특성을 이해하고, 전자기파를 설계하고 제어하는 기술을 개발할 수 있습니다.
2. 수식 기호별 의미:
- ∇: Nabla 연산자로, 벡터장의 그래디언트, 발산, 회전을 계산하는 연산자입니다.
- ×: 벡터곱으로, 벡터 두 개의 외적을 나타내며, 벡터 연산 결과로 새로운 벡터를 생성합니다.
- E: 전기장 벡터입니다.
- B: 자기장 벡터입니다.
- t: 시간입니다.
따라서 ∇×(∇×E)는 E 벡터장의 회전에 대한 그래디언트의 회전을 의미하며, ∂/∂t(∇×B)는 시간의 변화에 따른 B 벡터장의 회전을 의미합니다.
3. 활용방안:
맥스웰의 파동방정식은 전자기장과 전자기파의 특성을 이해하는 데 매우 중요합니다. 이 방정식은 전자기파의 전파속도, 굴절, 반사, 굴절 등을 설명하는 데 사용됩니다. 또한 이 방정식은 전자기장이 특정 장치나 회로에서 어떻게 작동하는지 이해하는 데 도움이 됩니다. 이를 통해 전자기장의 특성을 이해하고, 전자기파를 설계하고 제어하는 기술을 개발할 수 있습니다.
맥스웰의 파동방정식은 전자기장과 전자기파의 특성을 이해하는 데 매우 중요합니다. 이 방정식은 다양한 분야에서 활용됩니다.
1) 전자기파 통신: 전자기파 통신에서는 맥스웰의 파동방정식을 이용하여 전자기파를 생성하고 수신합니다. 전자기파의 주파수와 파장, 전파속도 등을 이용하여 통신을 설계합니다. 또한, 전자기파가 장애물이나 지표면 등을 만나서 굴절, 반사, 굴절 등이 일어나는 현상도 맥스웰의 파동방정식을 이용하여 설명할 수 있습니다.
2) 전자기장 해석: 전자기장이 특정 장치나 회로에서 어떻게 작동하는지 이해하는 데에도 맥스웰의 파동방정식을 활용합니다. 예를 들어, 트랜스포머나 인덕터에서의 전기장과 자기장의 상호작용은 맥스웰의 파동방정식을 이용하여 설명할 수 있습니다. 또한, 전기장이 이온화된 기체에 어떻게 작용하는지 이해하는 데에도 맥스웰의 파동방정식을 활용합니다.
3) 광학: 광학에서는 맥스웰의 파동방정식을 이용하여 빛의 전자기파를 설명합니다. 빛의 파장, 굴절, 반사, 굴절 등을 맥스웰의 파동방정식을 이용하여 설명할 수 있습니다. 또한, 광학기기의 작동원리도 설명할 수 있습니다.
4) 전자기장 제어: 전자기장을 제어하는 기술에서도 맥스웰의 파동방정식을 활용합니다. 예를 들어, 전자기파를 이용하여 물체를 가열하는 기술에서는 맥스웰의 파동방정식을 이용하여 전자기장을 제어합니다. 또한, 전자기장을 이용하여 전자를 가속하는 기술에서도 맥스웰의 파동방정식을 활용합니다.
이러한 방식으로 맥스웰의 파동방정식은 다양한 분야에서 활용됩니다. 이를 통해 전자기장의 특성을 이해하고, 전자기파를 설계하고 제어하는 기술을 개발할 수 있습니다.
4. Code:
from mayavi import mlab
from scipy import signal
# 공간 및 시간 변수 정의
x, y, z = np.mgrid[-10:10:100j, -10:10:100j, -10:10:100j]
t = np.linspace(0, 10, 100)
# 파동 함수 정의 (이 부분은 실제 전자기장 계산으로 대체될 수 있습니다)
def wave(x, y, z, t):
r = np.sqrt(x**2 + y**2 + z**2)
return np.sin(r - t)
# 시각화
mlab.figure(size=(800, 800))
for i in range(len(t)):
u = wave(x, y, z, t[i])
mlab.clf() # 이전 그래프 지우기
contour = mlab.contour3d(u, contours=8, transparent=True)
mlab.title('time: %.02f' % t[i])
# 범례 추가
mlab.colorbar(contour, title='Wave Amplitude', orientation='vertical')
mlab.show()
mlab.show()
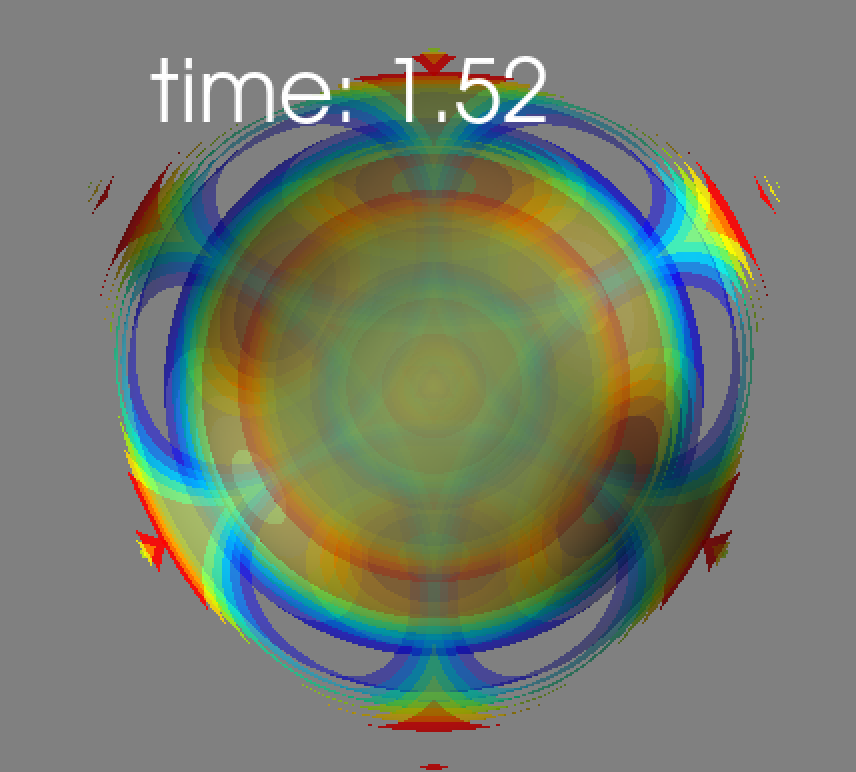
5. Code 설명 및 결과:
위 코드에서는 파동 함수를 정의하고, 시간에 따라 파동의 진행을 시각화하여 보여주고 있습니다. 이 파동 함수는 전자기장 계산 등에서 사용될 수 있는데, 파동 방정식 ∇×(∇×E) + ∂/∂t(∇×B) = 0은 이러한 파동의 진행을 나타내는 방정식입니다.
이 식은 시공간 상에서 E와 B의 회전과 변화를 나타내며, 파동의 전달에 영향을 미치는 중요한 역할을 합니다. 파동 함수는 이러한 E와 B의 변화를 나타내는데, 시간 t에 따라 파동 함수를 계산하여 파동의 진행을 시각화하고 있습니다.
특히, 파동 함수는 식에서 언급된 E와 B의 회전과 변화를 나타내므로, 파동 함수를 계산하고 이를 3D contour plot으로 시각화함으로써, 파동의 진행에 대한 직관적인 이해를 돕는데 도움이 됩니다.
따라서 이 예제 코드는 파동 방정식을 시각적으로 이해하는데 도움을 주는 것뿐 아니라, 파동 함수를 계산하여 전자기장 계산 등에서 사용될 수 있는 실제적인 계산에도 적용될 수 있습니다.


'[Python][Physics]' 카테고리의 다른 글
| [Python][Physics]#21 복소 지수 형태의 전자기파 파동식 해석(시각화) (0) | 2023.05.11 |
|---|---|
| [Python][Physics]#20 평면파 식(Plane wave equation)의 이해(시각화) (0) | 2023.05.11 |
| [Python][Physics]#18 입자 분포 밀도와 자유 입자 밀도의 합산으로 나타낸 총 밀도 함수(시각화) (0) | 2023.05.09 |
| [Python][Physics]#17 Ampere's law의 전류 밀도에 따른 자기장 회전(시각화) (0) | 2023.05.08 |
| [Python][Physics]#16 Faraday's Law의 전자기 유도 현상 (시각화) (0) | 2023.05.08 |